How To Find The Area Of A Weird Shape

Area of irregular shapes

To find the area of irregular shapes, the first thing to do is to divide the irregular shape into regular shapes that y'all can recognize such as triangles, rectangles, circles, squares and so forth...

Then, find the area of these individual shapes and add them up!

Example #one:

The figure above has ii regular shapes. It has a square and half a circle

Find the area for each of those ii shapes and add the results

Square

Area of the square = due south²

Area of the square = four²

Surface area of the square = 16

Circle

Area of the circumvolve = pi × r²

Notice that the radius of the circumvolve is iv/2 = 2

Area of the circle = three.14 × two²

Area of the circumvolve = three.14 × 4

Area of the circle = 12.56

Since you lot but have half a circumvolve, y'all have to multiply the result by one/2

Area of the one-half circle = ane/ii × 12.56 = 6.28

Area of this shape = 16 + six.28 = 22.28

Case #two:

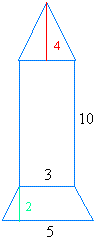
The figure above has iii regular shapes. Starting from top to bottom, it has a triangle, a rectangle, and a trapezoid

Find the area for each of those three shapes and add the results

Triangle

Area of the triangle = (base × height)/2

Area of the triangle = (3 × 4)/two

Area of the triangle = 12/two

Expanse of the triangle = 6

Rectangle

Area of the rectangle = length × width

Area of the rectangle = 3 × x

Area of the rectangle = 30

Trapezoid

Area of the trapezoid = ((b₁ + b_two) × h)/2

Area of the trapezoid = ((three + v) × 2)/2

Surface area of the trapezoid = (8) × 2/ii

Area of the trapezoid = 16/2

Area of the trapezoid = eight

Area of this shape = half dozen + 30 + 8 = 44

Example #three:

The expanse of irregular shapes can be as challenging equally this concluding instance, so study it carefully!

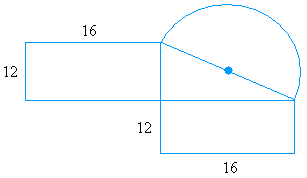
The effigy above has 4 regular shapes. Information technology has a triangle, 2 rectangles, and half a circle

Find the area for each of those 4 shapes and add together the results

Rectangle

Area of the rectangle = length × width

Area of the rectangle = (12 × xvi)

Expanse of the rectangle = 192

Since we have ii of the same rectangle, the area is 192 + 192 = 384

Triangle

Detect that the longest side of the rectangle is the base of the triangle and the short side of the rectangle is the height of the triangle

Then,

Area of the triangle = (base × acme)/2

Area of the triangle = (16 × 12)/2

Area of the triangle = (192)/ii

Area of the triangle = 96

Circle

To get the area of the half circle, we need to know the diameter

Notice that the diameter is the hypotenuse of a correct triangle, so use the Pythagorean Theorem to discover the length of the bore

c² = a^two + b^two

cⁱⁱ = 12² + 16^two

c² = 144 + 256

c^two = 400

c = √400

c = 20

Therefore, the diameter is xx. Since the bore is 20, the radius is 10

Area of the circle = pi × r²

Area of the circle = 3.fourteen × 10^two

Area of the circumvolve = iii.fourteen × 100

Area of the circle = 314

Since you just accept half a circle, yous accept to multiply the event past 1/2

one/2 × 314 = 157

Surface area of this shape = 384 + 96 + 157 = 637

Here we go! I promise these adept examples were very helpful in helping you how to get the expanse of irregular shapes.

Any questions on how to get the surface area of irregular shapes? Contact me.

Source: https://www.basic-mathematics.com/area-of-irregular-shapes.html

Posted by: haneywhick1943.blogspot.com

Share this post